

Preface
이 문서는 중국어 원서인 “입문 Visual SLAM 이론에서 연습까지 14 강(视觉SLAM十四讲 从理论到实践)” 책의 원저자로부터 한글 번역 허가를 받고 구글 번역기를 이용하여 작성된 문서입니다. 본 문서는 아래의 Contribution을 특징으로 합니다.
- 중국어 전공 서적을 구글 번역기를 이용해 한글로 초벌 번역했습니다.
- 초벌 번역 후 매끄럽지 않은 문장은 문맥에 맞게 수정되었습니다.
- 문서 내용 중 참고할만한 웹문서를 코멘트로 추가했습니다.
- SLAM 연구에서 주로 사용되는 용어는 한글로 번역된 용어보다 주로 사용되는 영어로 된 용어 그대로 표시하였습니다.
그럼에도 불구하고 부정확하거나 매끄럽지 않은 부분이 있을 수 있습니다. 그런 부분은 코멘트로 제안해주시면 반영하도록 노력하겠습니다. 또한 읽으시다가 잘 이해가 가지 않는 부분도 코멘트로 질문해주시면 답변해드리도록 하겠습니다.
번역 참가자:
신동원 (前 광주과학기술원 박사과정)
김선호 (前 VIRNECT 선임연구원)
조원재 (前 일본국립농업기술혁신공학센터 연구원)
장형기 (前 Imperial College London 석사과정)
박준영 (前 광주과학기술원 석사과정)
2018년 10월 1일
신동원 드림
제3장. 3차원 공간 강체 변환
|
주요 목표 |
지난 강의에서 Visual SLAM의 프레임워크와 내용에 대해 설명했습니다. 이 강의에서는 Visual SLAM의 근본적인 문제 중 하나인 3차원 공간에서 강체의 움직임이 어떻게 기술되는지를 설명합니다. 우리는 이것이 회전과 이동으로 구성된다는 것을 알고 있습니다. 이동 변환은 선형 변환이므로 문제가 많지 않지만 회전 변환은 다루기 어렵습니다. 이 장에서는 회전 행렬, 쿼터니언, 오일러 각의 의미와 그 계산 방법 및 변환 방법을 소개합니다. 실습에서는 선형 대수학 라이브러리 Eigen을 소개합니다. C ++에서 행렬 연산을 제공하며 Eigen의 Geometry 모듈은 쿼터니언과 같은 강체 운동에 대한 설명을 제공합니다. Eigen의 최적화는 완벽하지만 이를 사용하는 특별한 방법이 있습니다. 이는 실습에서 소개할 것입니다.
도움이 되는 유튜브 강의:
Lecture 2: Visual Navigation for Flying Robots
What are quaternions, and how do you visualize them? A story of four dimensions.
3.1 회전 행렬
3.1.1 점과 벡터, 좌표계
우리의 일상 생활 공간은 3차원이므로 우리는 3차원 공간의 움직임에 익숙합니다. 3차원 공간은 3개의 축으로 구성되므로 공간상의 점의 위치는 3개의 좌표로 지정할 수 있습니다. 그러나 우리는 이제 위치뿐만이 아니라 자신의 자세를 가진 강체(rigid-body)를 고려해야 합니다. 예를 들어 "카메라가 공간 (0,0,0)의 지점에 있으며 앞을 바라보고 있다."라고 말할 수 있습니다. 이것을 수학적인 언어로 표현해 봅시다.
먼저 포인트와 벡터의 기본부터 살펴 보겠습니다. 포인트의 기하학적 의미는 이해하기 쉽습니다. 3차원 공간상의 점이고 3개의 숫자로 표현됩니다. 하지만 벡터는 무엇일까요? 원점에서 어딘가를 가리키는 화살표로 생각할 수 있습니다. 벡터 a가 공간상에 있다고 생각해봅시다. 이 3차원 공간에서 좌표계를 지정할 때만이 좌표계에서 벡터의 좌표를 말할 수 있습니다. 즉 이 벡터에 해당하는 여러 실수를 찾을 수 있습니다.
예를 들어, 3차원 공간에서 벡터의 좌표는 $\mathbb{R}^3$ 의 세 숫자로 설명 할 수 있습니다. 우리가 선형 공간에 있다고 가정해보면, 기초가 되는 좌표계인 $ (\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3) $ 를 찾을 수 있습니다. 기초가되는 좌표계를 결정하면 이 기본 집합에서 벡터 a의 좌표를 말할 수 있습니다.

여기에서 $ (a_ 1, a_ 2, a_ 3 )^ \mathrm {T} $는 a의 좌표라고 불립니다. 따라서 좌표의 특정 값은 벡터 자체와 관련이 있으며 기초가 되는 좌표계의 선택과 관련이 있습니다. 3차원 공간상에서 좌표계는 대개 3개의 직교 축으로 구성됩니다. 예를 들어 x 축과 y 축이 주어지면 z 축은 오른손 (또는 왼손) 규칙에 의해 $ \mathbf {x} \times \mathbf {y} $로 정의될 수 있습니다. 좌표계는 정의된 방식에 따라 왼손 좌표계와 오른손 좌표계로 나뉩니다. 왼손 좌표계의 세 번째 축은 오른손 좌표계와 반대입니다. 대부분의 3D 라이브러리는 오른손 좌표계 (예 : OpenGL, 3D Max 등)를 사용하며 일부 라이브러리는 왼손 좌표계(예 : Unity, Direct3D 등)를 사용합니다.
기본적인 선형 대수학 지식을 바탕으로 벡터와 벡터, 벡터와 숫자 사이의 연산, 예를 들어 숫자 곱하기, 더하기, 빼기, 내적 곱, 외적 곱 등에 대해 이야기할 수 있습니다. 곱셈과 네 가지 연산은 아주 기본적이므로 여기서 반복하지 않습니다. $ \mathbf {a}, \mathbf {b} \in \mathbb {R}^ 3 $의 경우 $\mathbf{a}, \mathbf{b}$의 내적은 다음과 같이 쓸 수 있습니다.
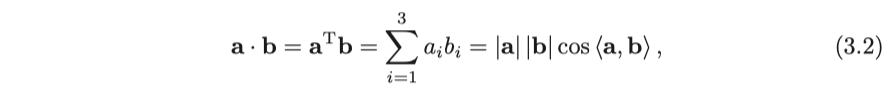
$ \left \langle { \mathbf {a}, \mathbf {b}} \right \rangle $는 벡터 a, b 사이의 각도를 나타냅니다. 또한 내적은 두 벡터 간의 투영 관계를 설명 할 수 있습니다.
다음으로 외적은 다음과 같습니다.

외적의 결과는 그 방향이 두 벡터에 수직이고 그 길이는 $ \left | \mathbf{a} \right | \left | \mathbf{b} \right | \left \langle { \mathbf {a}, \mathbf {b}} \right \rangle $이며 두 벡터에 의해 형성된 사변형의 방향 영역입니다. 외적의 경우 에는 벡터 a를 skew-symmetric matrix로 만드는 $ ^ \wedge $ 연산자를 활용할 수 있습니다. $ ^ \wedge $를 skew-symmetric symbol로서 쓸수 있습니다. 외적 $ \mathbf{a} \times \mathbf{b} $ 는 행렬 a와 벡터 b의 곱셈 $ { \mathbf{a}^ \wedge } \mathbf{b} $으로 쓰이며 선형 연산이 됩니다. 이 기호는 나중에 자주 사용되므로 기억해주십시오. 이 기호는 one-to-one mapping(전단사)으로서 모든 벡터에 대해 고유 한 반대 칭 행렬이 존재하고 그 반대의 경우도 마찬가지입니다.

3.1.2 유클리드 변환
우리는 종종 실제 환경에서 다양한 좌표계를 정의합니다. 로봇 공학에서는 각 링크와 관절에 대해 하나의 좌표계를 정의하고 3D 매핑에서는 각 입방체와 원통에 대한 좌표계도 정의합니다. 움직이는 로봇을 고려하면 그림 3-1에 정의된 $x_W, y_W, z_W$와 같이 고정된 것으로 간주할 수 있는 관성 좌표계 (또는 세계 좌표계)를 설정하는 것이 일반적입니다. 동시에 카메라 또는 로봇은 $x_C, y_C, z_C$로 정의된 좌표계와 같은 움직이는 좌표계입니다. 우리는 다음과 같은 질문을 할 수 있습니다. 카메라 좌표계에서 볼 수 있는 포인트 p는 카메라 좌표계에서 좌표 $\mathbf{p}_c$를 가지고 있습니다. 그리고 세계 좌표계에서 좌표는 $ \mathbf {p}_w$입니다. 그러면 이 두 좌표 간의 변환은 어떻게 될까요? 이때 먼저 로봇의 카메라 좌표계에서 포인트의 좌표 값을 구한 다음 로봇의 카메라 포즈를 활용해 세계 좌표계로 변환해야 합니다. 이 변환을 설명하는 수학적 방법이 필요합니다. 나중에 살펴 보겠지만 우리는 행렬 T로 설명할 수 있습니다.
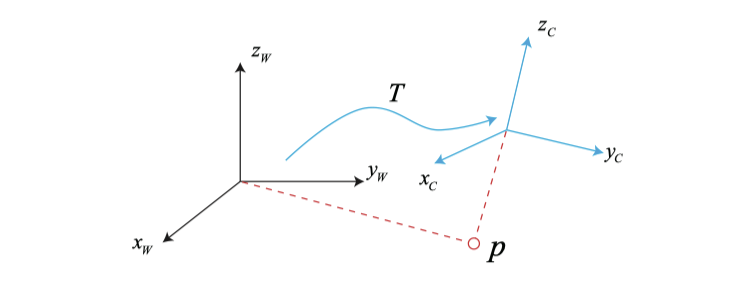
다음으로 두 좌표계 사이의 모션은 회전과 변환으로 구성되고 이를 rigid body motion이라고합니다. 확실히 카메라 모션은 좌표계 상의 벡터에 대한 길이와 각도가 변경되지 않는 rigid body motion입니다. 이 변환을 유클리드 변환이라고 합니다. 예를 들어 스마트폰을 공중에 던지면 지상에 떨어지기 전에 공간적 위치와 자세에 차이가 있을 수 있지만 스마트폰의 길이, 각 면의 각도 등은 변경되지 않습니다. 이 시점에서 우리는 스마트폰의 움직임이 유클리드 변환이라고 말합니다.
이러한 유클리드 변환은 회전과 변환의 두 부분으로 구성됩니다. 먼저 회전을 고려해봅시다. 우리는 단위 길이의 정규 직교 기저 $ ( \mathbf {e}_ 1, \mathbf {e}_ 2, \mathbf {e}_ 3 ) $ 설정하고 이 기저의 회전 후를 $ ( \mathbf {e}_ 1 ', \mathbf {e}_ 2 ', \mathbf {e}_ 3 ') $로 설정할수 있습니다. 그런 다음 동일한 벡터 a에 대해 각각의 두 좌표계에서의 좌표는 $ [a_ 1, a_ 2, a_ 3 ] ^ \mathrm {T} $ 와 $[a'_ 1, a'_ 2, a'_ 3 ]^ \mathrm {T} $로 나타낼 수 있습니다.
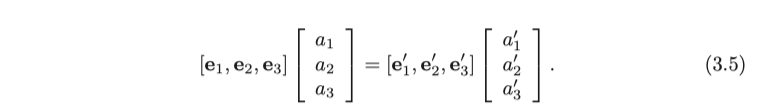
두 좌표 사이의 관계를 설명하기 위해, 위의 방정식의 좌변과 우변에 $ \left [ \begin {array}{l}
\mathbf{e}_1^\mathrm{T}\\
\mathbf{e}_2^\mathrm{T}\\
\mathbf{e}_3^\mathrm{T}
\end {array} \right ] $을 동시에 곱합니다. 그러면 좌변의 계수가 Identity 행렬이 됩니다. 따라서 :
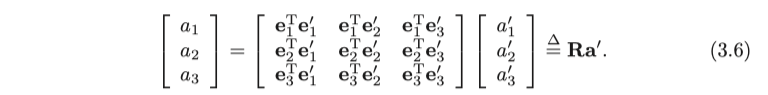
여기서 중간에 있는 행렬을 가져와서 행렬 R로 정의합니다. 이 행렬은 동일한 벡터의 회전 전과 후에 대한 좌표 변환 관계를 설명하는 두 기저 집합의 내적으로 구성됩니다. 행렬 R은 회전 자체를 설명한다고 말할 수 있습니다. 따라서 이를 회전 행렬이라고도 합니다. 이 행렬은 방향 코사인 행렬이라고도 하지만 우리는 이것을 회전 행렬이라고 통일하여 부를 것입니다.
회전 행렬에는 몇 가지 특별한 속성이 있습니다. 첫 번째로 회전 행렬은 행렬식의 값이 1인 직교 행렬입니다. 반대로 말해서, 이러한 행렬식을 갖는 직교 행렬은 회전 행렬이라고 할 수 있습니다. 따라서 다음과 같이 n 차원 회전 행렬 모음을 정의할 수 있습니다.

SO(n)은 Special Orthogonal Group의 의미입니다. 우리는 대수학의 개념인 "그룹(군)"의 설명 내용을 다음 장에서 하도록 하겠습니다. 이 집합은 n 차원 공간의 회전 행렬로 구성되며, 특히 SO(3)은 3차원 공간의 회전입니다. 행렬을 회전시킴으로써 두 좌표계 간의 회전 변환에 대해 직접 말할 수 있습니다. 즉, 회전 행렬은 카메라의 회전을 나타낼 수 있습니다.
회전 행렬은 직교 행렬이기 때문에 그 역 (즉, 전치)은 반대의 회전을 의미합니다. 위의 정의에 따르면, 다음과 같습니다 :
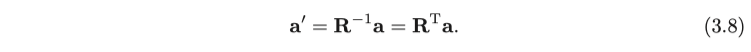
명시적으로 $ \mathbf{R}^\mathrm{T} $는 반대 방향의 회전을 나타냅니다.
유클리드 변환에는 회전 이외에 이동 변환이 있습니다. 세계 좌표계에서 벡터 a를 생각해봅시다. 회전 R과 이동 t에 의해 변환된 벡터 a’가 다음과 같이 계산될 수 있습니다.

여기서 t는 이동 벡터라고 합니다. 회전과 비교하여 변환 부분은 단순히 회전 후 좌표에 변환 벡터를 추가하기 때문에 매우 간단합니다. 위의 공식으로 회전 행렬 R과 평행 이동 벡터 t를 사용하여 유클리드 공간의 좌표 변환 관계를 완전히 설명합니다. 우리는 좌표계 1과 좌표계 2를 정의하고 각각의 두 좌표계 아래의 벡터 a는 $ \mathbf{a}_1, \mathbf{a}_2 $로 표현되며 둘 사이의 관계는 다음과 같아야 합니다.

여기에서 $ \mathbf{R}_{12} $는 "좌표계 2에서 좌표계 1 로의 회전"을 의미합니다. 벡터는 이 행렬의 오른쪽으로 곱해 지므로 아래 첨자는 오른쪽에서 왼쪽으로 읽습니다. 이것은 이 책에서 활용하는 관습적인 방법 일뿐입니다. 좌표 변환은 특히 여러 좌표계가 있는 경우 혼동하기 쉽습니다. 마찬가지로 "좌표계 1에서 좌표계 2로의 회전 "을 표현하려면 $ \mathbf{R}_{21}$로 씁니다. 책마다 표기법이 다르며 어떤 책은 왼쪽 상단 / 아래 첨자로 기록하기도 하므로 독자는 여기서 표기법에 대해 명확하게 이해해야 합니다.
$\mathbf{t}_{12}$은 실제로는 좌표계 1에서 좌표계 2의 원점을 가리키는 좌표계 1 원점에서의 벡터에 해당하며, 좌표계 1에서 좌표를 가져 오므로 독자들에게 "좌표계 1에서 좌표계 2까지의 벡터"라고 이해할 것을 제안합니다. 그러나 좌표계 2의 원점에서 좌표계 1의 원점까지의 벡터인 역방향 $ \mathbf{t}_{21} $은 좌표계 2에서 좌표를 가져오며 $-\mathbf{t}_{12}$와 같지 않고 두 시스템의 회전과 관련하여 생각해야 합니다. 따라서 초보자가 “내 좌표는 어디에 있습니까?”라는 질문을 할 때 이 문장의 의미를 명확하게 설명해야 합니다. 여기서 "내 좌표"는 일반적으로 로봇 시스템의 원점을 가리키는 월드 시스템의 벡터를 참조한 다음 월드베이스에서 좌표를 가져옵니다. 수학 기호에 따라 $ \mathbf{t}_{WC} $의 값이어야 합니다. 같은 이유로 $ - \mathbf {t}_{CW}$가 아니라 실제로는 $-\mathbf{R}_{CW}^T \mathbf{t}_{CW}$입니다.
3.1.3 변환 행렬 및 동차 좌표 (Transformation matrix and homogeneous coord.)
식 (3.9)은 유클리드 공간의 회전과 변환을 완전하게 표현하지만, 여기에서의 변환 관계는 선형 관계가 아니라는 문제가 있습니다. 우리가 $ \mathbf {R}_ 1, \mathbf {t}_ 1 $ 와 $ \mathbf {R}_ 2, \mathbf {t}_ 2 $를 이용해 다음의 두 가지 변환을 수행했다고 가정해봅시다.

그래서 a에서 c로의 변환은 다음과 같습니다.

이러한 형식은 여러 개의 변환이 연속적으로 진행되면 식이 너무 복잡해집니다. 따라서 homogeneous 좌표와 변환 행렬을 도입하여 식 (3.9)를 다음과 같이 다시 쓰고자 합니다.

이것은 하나의 수학적 기법입니다. 3D 벡터의 끝 부분에 1을 추가하고 homogeneous 좌표라는 4D 벡터로 변환합니다. 이러한 4차원 벡터의 경우 회전 및 이동 변환을 행렬로 작성하여 전체 관계를 선형으로 만들 수 있습니다. 이 공식에서 행렬 T는 변환 행렬이라고 부릅니다. 우리는 여기서 $ \mathbf {a} $의 Hhomogeneous 좌표를 나타내기 위해 $ \tilde { \mathbf {a} } $를 사용합니다. 그런 다음 homogeneous 좌표와 변형 행렬을 활용하여 연속적인 두 변환은 다음의 간략화된 형태로 표현할 수 있습니다.
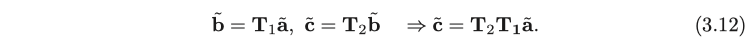
그러나 homogeneous와 non-homogeneous 좌표를 구별하는 기호는 수식을 이해하기 다소 어렵게 만듭니다. 왜냐하면 homogeneous 좌표계를 표현하기 위해 벡터의 끝에 1을 추가하거나 non-homogenous 좌표계를 표현하기 위해 1을 제거해야 합니다. 따라서 여기서 구분 없이 우리는 B = Ta로 직접 쓸 것입니다. 그리고 기본적으로 이를 homogenous 좌표로 활용합니다.
변형 행렬 T와 관련하여 특별한 구조가 있습니다. 왼쪽 상단 구석은 회전 행렬입니다. 오른쪽은 이동 벡터이고, 왼쪽 하단 모서리가 0이고 오른쪽 하단 모서리가 1입니다. 이 매트릭스는 Special Euclidean Group이라고도 합니다.

SO(3)과 마찬가지로 이 행렬의 역을 푸는 것은 역변환을 나타냅니다.

다시 말하지만 $ \mathbf{T}_{12} $ 표기법을 사용하여 좌표계 2에서 좌표계 1 로의 변환을 나타냅니다. 또한, 기호를 간결하게 유지하기 위해, 모호성이 없는 경우, homogeneous 좌표 및 ordinary 좌표의 기호는 이후 섹션에서 구별하지 않고 활용합니다. 예를 들어, 우리가 $ \mathbf {T} \mathbf{a} $를 쓸 때 우리는 homogenous 좌표를 사용합니다. $ \mathbf{Ra} $를 작성할 때는 non-homogenous 좌표를 사용합니다. 동일한 방정식으로 작성하면 homogenous 좌표에서 일반 좌표로의 변환이 이미 완료된 것으로 가정합니다. 왜냐하면 homogeneous 좌표와 non-honogeneous 좌표 간의 변환이 실제로 매우 쉽기 때문입니다. C++ 프로그램에서는 연산자 오버 로딩으로 이를 수행할 수 있습니다.
마치기 전에 본 절의 내용을 다시 한번 살펴보겠습니다. 먼저 벡터와 그 좌표 표현을 소개하고 벡터 간의 작업을 소개했습니다. 그런 다음 좌표계 사이의 움직임은 평행 이동과 회전으로 구성된 유클리드 변환으로 설명했습니다. 회전은 회전 행렬 SO(3)로 설명할 수 있으며, 변환은 $ \mathbb{R}^ 3 $ 벡터로 직접 설명했습니다. 마지막으로 이동과 회전이 행렬에 배치되면 변환 행렬 SE(3)가 형성됩니다.
3.2 연습 : Eigen
강의의 실습 부분에는 두 개의 섹션이 있습니다. 첫 번째 부분에서는 Eigen을 사용하여 행렬 및 벡터를 나타내는 방법을 설명하고 회전 행렬 및 변환 행렬의 계산으로 확장합니다. 이 섹션의 코드는 slambook2/ch3/useEigen에 있습니다.
Eigen은 C ++ 오픈 소스 선형 대수 라이브러리입니다. 방정식 풀이와 같은 함수뿐만 아니라 행렬에 대한 빠른 선형 대수 연산을 제공합니다. 많은 상위 소프트웨어 라이브러리인 g2o, Sophus는 Eigen을 포함하여 매트릭스 작업에 사용합니다. 이 강의의 이론적인 부분에서 Eigen의 프로그래밍에 대해 배워봅시다.
Eigen가 PC에 설치되어 있지 않을 수도 있으므로 다음 명령을 입력하여 설치해봅시다.

일반적으로 사용되는 라이브러리의 대부분은 Ubuntu 소프트웨어 소스에서 사용할 수 있습니다. 앞으로 라이브러리를 설치하려면 Ubuntu 소프트웨어 소스를 검색해야 할 수도 있습니다. apt 명령을 사용하면 Eigen을 쉽게 설치할 수 있습니다. 이전 강의를 되돌아보면 라이브러리는 헤더 파일과 라이브러리 파일로 구성된다는 것을 알고 있습니다. Eigen 헤더 파일의 기본 위치는 "/usr/include/eigen3/"입니다. 확실하지 않은 경우 다음 명령을 찾을 수 있습니다.

다른 라이브러리와 비교하여, Eigen은 순수한 헤더 파일로 빌드된 라이브러리라는 점에서 특별합니다 (이것은 놀랍습니다!). 즉,. so 또는 .a와 같은 이진 파일이 아닌 헤더 파일만 찾을 수 있습니다. 이 파일을 사용하면 Eigen의 헤더 파일 만 가져와야 하므로 라이브러리 파일이 없으므로 라이브러리 파일을 링크할 필요가 없습니다. Eigen을 실제로 사용하기 위해 아래 코드를 작성해봅시다.
Slambook2/ch3/useEigen/eigenMatrix.cpp
gaoxiang12/slambook
Contribute to gaoxiang12/slambook development by creating an account on GitHub.
github.com
이 예제는 Eigen 행렬의 기본 연산과 연산을 보여줍니다. 이것을 컴파일하기 위해서는 CMakeLists.txt에 Eigen의 헤더 파일 디렉터리를 지정해야 합니다 :

Eigen Library에는 헤더 파일만 있으므로 target_link_library 문을 사용하여 프로그램을 라이브러리에 연결할 필요가 없습니다. 그러나 대부분의 다른 라이브러리에서 대부분 링크 명령을 사용해야 합니다. 이후의 실습에서는 find_package 명령을 사용하여 라이브러리를 검색하지만 여기서는 조금 다르게 헤더 파일 디렉터리를 지정하는 것만으로 컴파일을 진행합니다. 프로그램을 컴파일한 후에 실행하면 각 매트릭스의 출력을 볼 수 있습니다.

자세한 설명이 코드에 제공되어 있으므로 명령문의 각 줄은 여기에서 설명하지 않습니다. 이 책에서는 몇 가지 중요한 위치에 대한 설명만 제공합니다 (뒷부분에서도 이 스타일을 유지합니다).
- 독자는 위의 코드를 실제로 입력해보고 테스트해보는 것이 것이 가장 좋습니다 (주석 제외). 적어도 위의 프로그램을 컴파일하고 실행하십시오.
- KDevelop는 불완전함으로 인해 발생하는 C++ 멤버 을 촉구하지 않을 수 있습니다. 위의 입력을 따르려면 Enter를 묻는 메시지가 나타나지 않으면 상관하지 마십시오. 클리닝은 당신에게 완전한 힌트를 줄 것입니다
- Eigen이 제공하는 행렬은 MATLAB과 매우 유사하며 거의 모든 데이터가 행렬로 처리됩니다. 그러나 효율성을 높이려면 Eigen에 있는 행렬의 크기와 유형을 지정해야 합니다. 컴파일 타임에 크기를 알고 있는 행렬의 경우 동적으로 변하는 행렬보다 빠르게 처리됩니다. 따라서 회전 행렬 및 변환 행렬과 같은 데이터는 크기와 데이터 유형에 따라 컴파일 시간에 결정될 수 있습니다
- Eigen 내부의 행렬 구현은 더 복잡합니다. 여기서는 소개하지 않을 것이며 float 및 double과 같은 내장 데이터 유형과 같은 Eigen 행렬을 사용할 수 있기를 바랍니다. 이것은 디자인의 원래 의도와 일치해야 합니다
- Eigen 행렬은 C ++의 빌트인 데이터 유형과는 다르게 automatic type promition을 지원하지 않습니다. C ++ 프로그램에서는 float 데이터와 double 데이터를 추가하고 곱할 수 있으며 컴파일러는 자동으로 데이터 유형을 가장 적합한 데이터 유형으로 변환합니다. Eigen에서는 성능상의 이유로 매트릭스 유형을 명시 적으로 변환해야 합니다. 그리고 이것을 잊어버리면, Eigen은 (아주 친숙하지는 않지만) " YOU MIXED DIFFERENT NUMERIC TYPES..."라는 컴파일 오류를 표시할 것입니다. 이 메시지가 나타나는 오류 메시지의 부분을 찾으려고 할 수 있습니다. 오류 메시지가 너무 길면 파일에 저장하고 찾아내는 것이 가장 좋습니다.
- 같은 방법으로 계산 과정에서 행렬 차원의 정확성을 보장해야 합니다. 그렇지 않으면 "YOU MIXED DIFFERENT NUMERIC SIZES"오류가 발생합니다. 이런 종류의 에러 메시지에 대해 불평하지 마십시오. C ++ 템플릿 메타 프로그래밍의 경우, 읽을 수 있는 정보를 프롬프트 할 수 있어서 매우 행운입니다. 나중에 Eigen의 오류가 발견되면 대문자 부분을 직접 보고 문제가 무엇인지 파악할 수 있습니다.
- 우리는 기본 행렬 작업만을 다룹니다. http://eigen.tuxfamily.org/dox-devel/modules.html에서 Eigen에 대해 자세히 알아보십시오. 여기서는 가장 간단한 부분만 설명합니다.
마지막 코드에서 역행렬 및 QR 분해의 효율이 비교됩니다. 자신의 컴퓨터에서 연산 시간의 차이를 볼 수 있습니다. 두 가지 방법 간에 연산 시간 측면에서 큰 차이가 있나요?
3.3 회전 벡터와 오일러 각
3.3.1 회전 벡터
다시 이론적인 부분으로 돌아가 봅시다. 회전을 설명하는 회전 행렬을 사용하면 6 자유도의 3차원 강체 모션을 나타내는 4X4 변환 행렬만 있으면 충분할까요? 여기서 회전 행렬 표현은 적어도 다음과 같은 단점이 있습니다.
- SO(3)의 회전 행렬은 9 개의 숫자를 갖지만 하나의 축에 대한 회전에 대해 3 자유도만 있습니다. 따라서 이 표현은 중복됩니다. 유사하게, 변환 행렬은 16개의 값으로 6 자유도 변환을 표현합니다. 더 콤팩트한 표현이 없을까요?
- 회전 행렬 자체에는 제약 조건이 있습니다. 이 행렬은 행렬식이 1인 직교 행렬이어야 합니다. 이는 변환 행렬에서도 마찬가지입니다. 이러한 제약 조건은 회전 행렬 / 변환 행렬을 추정하거나 최적화할 때 설루션 찾는 것을 더 어렵게 만듭니다.
따라서 회전 및 이동을 간결하게 설명하는 방법이 있기를 바랍니다. 예를 들어, 3차원 벡터로 회전을 표현하고 6차원 벡터로 변환을 표현하는 것이 가능할까요? 사실, 우리는 앞에서 외적을 도입 한 섹션에서 이를 수행하는 방법을 언급했습니다. 우리는 두 벡터의 회전 관계를 표현하기 위해 외적을 사용하는 방법을 소개했습니다. 좌표계의 회전을 위해 회전은 회전축과 회전 각으로 설명될 수 있습니다. 따라서 방향이 회전 축과 일치하고 길이가 회전 각도와 동일한 벡터를 사용할 수 있습니다. 이 벡터를 회전 벡터라고 합니다. 이 표현은 회전을 설명하는 데 3차원 벡터만 있으면 됩니다. 유사하게, 변환 행렬에 대해서, 변환을 표현하기 위해 회전 벡터와 변환 벡터를 사용합니다. 이 벡터의 차수는 정확히 6차원입니다 (회전 3 + 이동 3 = 6차원).
사실, 회전 벡터는 다음 장에서 소개할 Lie 대수학과 관련이 있습니다. 이 내용은 다음 장을 위해 남겨 둡시다. 이 장에서 독자는 회전이 그렇게 표현될 수 있다는 것만 알고 넘어가면 됩니다. 회전 행렬 R로 표시되는 회전을 고려해봅시다. 회전축이 단위 길이 벡터 n이고 각도가 θ라고 가정하고 회전 벡터로 설명하면 벡터 θn은 회전을 설명할 수 있습니다. 그래서 우리는 두 표현의 사이의 연관성이 무엇인지 물어봐야 합니다. 사실, 그들의 전환 관계를 도출하는 것은 어렵지 않습니다. 회전 벡터에서 회전 행렬로의 변환 프로세스는 Rodrigues의 공식으로 표시됩니다. 하지만 유도 과정이 더 복잡하기 때문에 이를 설명하지 않고 변환 결과만 제공합니다.

기호 ^는 반대칭 변환에 대한 벡터이며 식 (3.3)을 참조하십시오 (벡터의 외적 표현). 반대의 연산도 다음의 수식을 이용해 계산할 수 있습니다.

따라서 :

회전축 n에 관해서는, 회전축 상의 벡터는 회전 후에 변화하지 않기 때문에,

따라서 회전축 n은 행렬 R의 eigen value가 1에 해당하는 eigen vector입니다. 이 방정식을 풀고 정규화하면 회전축을 얻을 수 있습니다. 독자는 "회전축이 회전한 후에도 변하지 않습니다"라는 기하학적 점에서 이 방정식을 볼 수 있습니다. 여기에 있는 두 가지 변환 공식은 여전히 다음 장에서 설명할 것이며, 당신은 Lie 그룹과 Lie 대수학의 SO (3)에 대한 일치임을 알게 될 것입니다.
3.3.2 오일러 각
오일러 각에 대해서 이야기해봅시다.
회전 행렬이나 회전 벡터는 회전을 설명할 수 있지만 인간에게는 직관적으로 잘 와 닿지 않습니다. 회전 행렬 또는 회전 벡터를 볼 때 이 회전이 무엇인지 상상하기 어렵습니다. 그들이 변화할 때 우리는 물체가 어느 방향으로 돌고 있는지 알지 못합니다. 이때, 오일러 각은 회전을 설명하는 매우 직관적인 방법을 제공합니다. 3개의 기본 축을 사용하여 회전을 다른 축을 중심으로 3 개의 회전으로 분해합니다. 인간은 단일 축을 중심으로 회전하는 과정을 쉽게 이해할 수 있습니다. 그러나 다양한 분해 방법으로 인해 오일러 각도에 대해 다양하고 혼란스러운 정의 방법이 많이 있습니다. 예를 들어, 먼저 X 축을 중심으로 회전 한 다음 Y 축을 중심으로, 마지막으로 Z 축을 중심으로 회전할 수 있습니다. 이렇게 하면 XYZ 순서와 같은 회전을 얻을 수 있습니다. 마찬가지로 ZYZ 및 ZYX와 같은 회전 순서를 정의할 수 있습니다. 또한 고정 축을 중심으로 회전하는지 아니면 회전 후 축을 중심으로 회전하는지 구별해야 합니다. 그러면 다른 정의도 제공됩니다.
회전축 순서의 이러한 불확실성은 많은 실제적인 어려움을 가져옵니다. 다행스럽게도 특정 연구 분야에서, 오일러 각은 대개 일반적인 정의를 가지고 있습니다. 항공기 및 모델 항공기에서 "피치각"및 "요각"이라는 단어를 들었을 수 있습니다. 가장 일반적인 유형의 오일러 각 중 하나는 요우, 피치, 롤 (yaw-pitch-roll)의 세 가지 각도로 회전을 설명하는 것입니다. 이는 ZYX 축의 회전과 동일하므로 ZYX를 예 로들 수 있습니다. 강체의 앞면이 X 축이고, 오른쪽이 Y 축이고, 맨 위가 Z 축이라고 가정합니다 (그림 3-2 참조). 그러면 ZYX 회전 각은 임의의 회전을 다음 세 축으로 나누는 것과 같습니다.
- 객체의 Z 축을 중심으로 회전하여 요각을 얻습니다.
- 회전 후에 Y 축을 중심으로 회전하여 피치각을 얻습니다.
- 회전 후에 X 축을 중심으로 회전하여 롤각을 얻습니다.
이 시점에서 우리는 $[r,p,y]^\mathrm{T}$와 같은 3차원 벡터를 사용하여 임의의 회전을 설명할 수 있습니다. 이 벡터는 매우 직관적이며이 벡터의 회전 과정을 상상할 수 있습니다. 이런 방식으로, 다른 오일러 각도 3차원 벡터를 얻기 위해 3개의 축으로 분해되지만, 선택된 축과 선택 순서는 다릅니다. 여기에 소개된 rpy 각도는 일반적인 방법 중 하나이며, 소수의 오일러 각도만 rpy와 같은 이름을 갖습니다. 다른 오일러 각은 회전축의 순서로 참조됩니다. 예를 들어 rpy 각도의 회전 순서는 ZYX입니다. 마찬가지로 XYZ, ZYZ와 같은 오일러 각도 있지만 특별한 이름은 없습니다. 오일러 각을 사용할 때 대부분의 영역에는 고유 한 좌표 방향 및 순서 습관이 있음을 언급할 필요가 있습니다. 이는 우리가 여기서 말한 것과 반드시 같지는 않습니다.
오일러 각의 주요 단점은 유명한 Gimbal Lock이 발생한다는 것입니다. 피치 각이 $\pm 90 ^\circ $일 때 첫 번째 회전과 세 번째 회전은 동일한 축을 사용하므로 시스템의 자유도가 손실됩니다. 이를 특이성 문제라고 부르며 오일러 각의 다른 형태에도 존재합니다. 이론적으로 3차원 회전을 표현하기 위해 3개의 실수를 사용하고자 한다면 필연적으로 특이점 문제가 발생한다는 것을 증명할 수 있습니다. 이 원리로 인해, 오일러 각은 보간과 반복에 적합하지 않으며 종종 human-computer interaction에만 사용됩니다. 또한 SLAM 프로그램에서 직접 포즈를 표현하기 위해 오일러 각도를 거의 사용하지 않으며 필터링 또는 최적화에서 회전을 표현하는 데 오일러 각도를 사용하지 않습니다 (특이점 문제가 있기 때문에). 그러나 알고리즘이 잘못되었는지 확인하려면 오일러 각으로 변환하면 신속하게 결과를 확인할 수 있습니다.

3.4 쿼터니언
회전 행렬은 3가지 자유도를 9개의 값으로 회전시키므로 중복성을 가지며 오일러 각도와 회전 벡터는 그런 중복성은 없지만 Gimbal Lock과 같은 문제가 있습니다. 사실 우리는 특이점(singularity) 문제가 없는 3차원 벡터 기술방법을 찾을 수는 없습니다 [19].
우리가 예전에 공부한 복소수를 생각해봅시다. 우리는 복소수 집합 $ \mathbb {C} $를 사용하여 2D 복소평면의 벡터를 나타냅니다. 단위 복소수의 복소수 곱셈은 2D 평면에서 회전을 나타낼 수 있습니다. 예를 들어 복소수 $i$를 곱하는 것은 복소수 벡터를 반 시계 방향으로 $ 90 ^ \circ $ 회전하는 것과 동일합니다. 유사하게, 3차원 공간에서의 회전을 표현할 때, 복소수와 유사한 대수적 표현인 쿼터니언(Quaternion)도 있습니다. 쿼터니언은 해밀턴이 찾은 확장된 복소수이며, 콤팩트하고 singularity가 없습니다. 그러나 쿼터니언은 직관적이지 않으며, 그 동작은 이해하기 좀 더 복잡합니다.
쿼터니언을 복소수와 비교하면 쿼터니언을 더 빨리 이해할 수 있습니다. 예를 들어, 복소수 평면의 벡터를 $\theta$만큼 회전시키려는 경우, 극좌표 좌표로 표시된 복소수 인 $\mathrm{e}^{i \theta}$로 복소수 벡터를 곱할 수 있습니다. 그것은 또한 유명한 오일러 방정식과 같은 일반적인 형태로 작성될 수 있습니다.

이것은 단위 길이의 복소수입니다. 따라서, 2차원의 경우, 단위 복소수로 회전을 설명할 수 있습니다. 마찬가지로, 3D 회전을 단위 쿼터니언으로 설명 할 수 있음을 알 수 있습니다.
쿼터니온 q는 하나의 실수 부와 세 개의 허수 부를 갖습니다. 이 책은 다음과 같이 실수 부분을 앞에 씁니다.
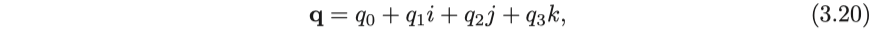
여기서 $ i,j,k $는 쿼터니언의 세 가상 부분입니다. 이 3개의 가상 부분은 관계를 충족시킵니다.
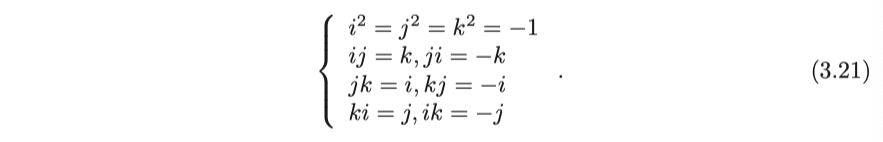
이 특별한 표현 때문에, 사람들은 때로 쿼터니언을 표현하기 위해 스칼라와 벡터를 사용합니다.
우리가 $ i, j, k $를 3 축으로 보면, 복소수의 곱셈과 외적이 동일합니다. 때로는 사람들이 스칼라와 쿼터니언을 표현하는 벡터를 사용합니다.
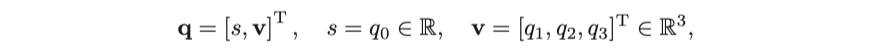
여기서 s는 quaternion의 실수부라고 불리며, v는 그것의 허수부라고 불립니다. 특별히 허수 부분이 0 인 경우, 그것은 real 쿼터니언이라고 불립니다. 반대로, 실수 부분이 0이면 이를 imaginary 쿼터니언이라고 합니다.
단위 쿼터니언을 사용하여 3차원의 회전을 표현할 수 있지만 이 표현은 복소수와 미묘하게 다릅니다. 복소수에서 $ i $를 곱하는 것은 90도 회전하는 것을 의미합니다. 이것은 $ i $를 곱하는 것이 쿼터니언에서 $ i $ 축 주위로 90도 회전된다는 것을 의미합니까? 그래서, $ ij = k $는 $ i $를 중심으로 90도 회전 한 다음 $ j $를 90도 회전시키는 것이 $ k$를 중심으로 90도와 동일하다는 것을 의미합니까? 독자는 실제 물체를 사용하여 시뮬레이션해보면 이것이 사실이 아님을 알게 될 것입니다. 올바른 것은 $ ij=k $의 성질을 보장하기 위해 $ i $는 180도 회전에 대응해야 한다는 것입니다. 그리고 $ i^ 2 =- 1 $ 은 i 축을 중심으로 360도 회전한 후 반대 방향을 의미합니다.
이것은 약간 신비한 것 같습니다. 완전한 설명에는 너무 많은 추가 사항이 필요합니다. 진정하고 쿼터니언으로 돌아갑시다. 적어도 단위 쿼터니언이 3차원 공간의 회전을 표현할 수 있다는 것을 알고 있습니다. 그렇다면 쿼터니언의 속성은 무엇일까요? 그리고 그들은 어떻게 서로 작동할 수 있을까요?
3.4.2 쿼터니언 연산
쿼터니언은 일반 복소수와 유사하므로 일련의 연산을 수행할 수 있습니다. 두 개의 복소수를 사용하는 것처럼 쉽게 더하기, 빼기, 곱하기를 쿼터니언으로 수행할 수 있습니다. 각각 $ [s_a, \mathbf {v}_a]^ \mathrm {T}, [s_b, \mathbf{v}_b]^ \mathrm {T} $로 표현되는 2개의 쿼터니언 $ \mathbf{q}_a, \mathbf{q}_b $가 있다고 가정해봅시다.

쿼터니언 사이의 연산은 다음과 같이 나타낼 수 있습니다.
1. Addition and subtraction.
쿼터니언 $ \mathbf {q}_a, \mathbf {q}_b $의 더하기 및 빼기는 다음과 같습니다.

2. Multiplication.
곱셈은 $ \mathbf {q}_a $의 각 항목과 $ \mathbf {q}_b $의 각 항목의 곱셈이고, 마지막으로, 허수 부분은 식 (3.21)에 따라 수행됩니다.

조금 복잡하긴 하지만 양식은 깔끔하고 질서 정연합니다. 벡터 형식으로 작성되고 내적 및 외적을 사용하는 경우 표현식이 보다 간결 해집니다.
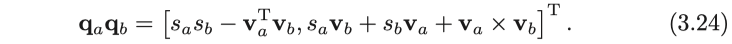
이 곱셈 정의에서 두 개의 real 쿼터니언 곱은 여전히 실수이며 실수에서의 곱셈과도 일치합니다. 그러나 마지막 외적의 존재로 인해, $ \mathbf {v}_a $와 $ \mathbf {v}_b $가 $ \mathbb {R}^ 3 $공간에서 평행하지 않으면 쿼터니언 곱셈은 일반적으로 교환 법칙이 성립하지 않습니다. 그러면 외적항은 0이 됩니다.
3. Length.
쿼터니언의 크기는 다음과 같이 정의됩니다.

쿼터니언 곱셈의 크기는 각 쿼터니언의 크기의 곱셈인 것을 확인할 수 있습니다. 이렇게 하면 단위 쿼터니언에 다른 단위 쿼터니언을 곱할 때 단위 길이를 유지하게 합니다.

4. Conjugate.
쿼터니언의 conjugate는 허수 부분을 반대로 취하는 것입니다.

쿼터니언에 이 것의 conjugate를 곱하면 실수 쿼터니언이 됩니다. 실수 부분은 크기의 제곱입니다.

5. Inverse.
쿼터니언의 inverse는 다음과 같습니다.

이 정의에 따르면, 쿼터니언과 그 inverse의 곱은 실수 쿼터니언 $ \mathbf {1} $입니다.

q가 단위 쿼터니언이면 이것의 inverse와 conjugate는 같습니다. 동시에 곱셈의 inverse는 행렬과 비슷한 특성을 갖습니다.

6. Scalar Multiplication.
벡터와 마찬가지로 쿼터니언은 숫자로 곱할 수 있습니다.

3.4.3 쿼터니언을 활용한 회전 표현
우리는 쿼터니언을 사용하여 점의 회전을 표현할 수 있습니다. 3차원 공간상의 점 $ \mathbf{p} = [x,y,z]^\mathrm{T} \in \mathbb {R}^3$ 와 회전은 단위 쿼터니언 $ \mathbf{q}$이라고 가정해봅시다. 3차원 점 $\mathbf{p}$는 회전 한 후 $\mathbf{p}'$가됩니다. 행렬 설명이 사용되면 $ \mathbf{p}'= \mathbf{R} \mathbf{p} $입니다. 회전을 설명하는 데 쿼터니언을 사용하는 경우 관계가 어떻게 표현될까요?

먼저, 3차원 점은 imaginary 쿼터니언으로 표현됩니다. 그러면 회전된 점 $ \mathbf {p}' $는 다음과 같은 곱셈으로 표현될 수 있습니다.

여기에 곱셈은 쿼터니언 곱셈이며 그 결과는 쿼터니언입니다. 마지막으로, 우리는 $ \mathbf{p}' $의 허수 부분을 가져 와서 회전 후 지점의 좌표를 얻습니다. 계산의 실제 부분이 0이므로 쉽게 확인할 수 있습니다. 따라서 이는 pure imaginary 쿼터니온입니다.
3.4.4 쿼터니언에서 회전 행렬로 변환
임의의 단위 쿼터니언은 회전을 설명하며 회전 행렬 또는 회전 벡터로 설명될 수도 있습니다. 이제 쿼터니언과 회전 벡터 / 행렬 간의 변환 관계를 살펴보겠습니다. 그전에 쿼터니언 곱셈은 매트릭스 곱셈으로 작성될 수도 있음을 인지해야합니다. $\mathbf{q}=[s,\mathbf{v}]^\mathrm{T}$라고 할때, $^{+}$ 와 $^{\oplus}$ 기호를 정의합니다 [20].

이 두 기호는 4 × 4의 행렬에 쿼터니언을 매핑합니다. 그런 다음 쿼터니언 곱셈은 매트릭스의 형태로 작성 될 수 있습니다.

간단히 표현하면
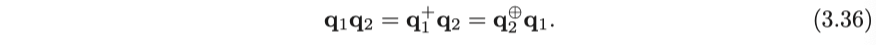
그런 다음 쿼터니언을 사용하여 공간상의 점을 회전시키는 문제를 생각해봅시다. 이전 장에 따르면, 다음과 같습니다.

두 기호에 해당하는 행렬을 대체하면 다음과 같이 됩니다.
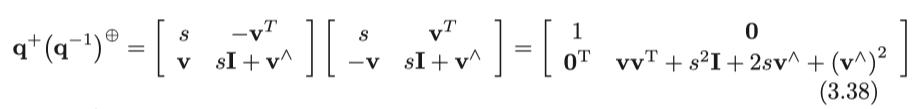
$\mathbf{p}'$ 와 $\mathbf{p}$는 둘 다 imaginary 쿼터니언 이므로 행렬의 오른쪽 아래 원소가 쿼터니언에서 회전 행렬로의 변환을 나타냅니다.

쿼터니언에서 회전 벡터로의 변환 공식을 얻기 위해 위 공식의 양쪽에서 트레이스를 취합니다.
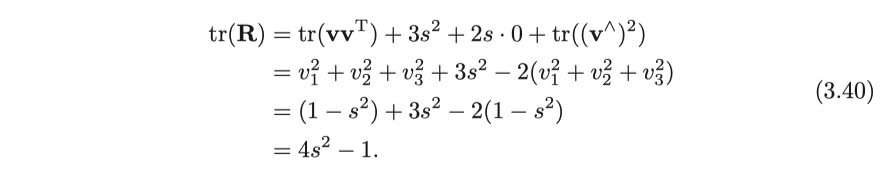
식 (3.17)에 의해서

여기서

그러므로

회전축의 경우 식 (3.38)에서 $\mathbf{q}$의 imaginary 부분을 $\mathbf{p}$로 교체하면 $\mathbf{q}$의 imaginary 부분이 회전 할 때 움직이지 않는 부분을 쉽게 알 수 있습니다. 즉, 정확히 회전 축을 구성합니다. $\mathbf{q}$의 imaginary 부분을 정규화하여 회전축을 얻을 수 있습니다. 요약하면, 쿼터니언에서 회전 벡터로의 전환 공식은 다음과 같이 작성할 수 있습니다.

다른 표현에서 쿼터니언으로 변환하는 방법은 위의 단계를 반대로 진행하면 됩니다. 실제 프로그래밍에서 라이브러리는 일반적으로 다양한 형식 간의 전환을 제공합니다. 쿼터니언, 회전 행렬 또는 각도 축이든, 모두 동일한 회전을 설명하는 데 사용할 수 있습니다. 우리는 특정한 양식을 붙이지 않고 가장 편리한 형태를 선택해야 합니다. 실습에서 실제로 다양한 회전 표현 간의 전환을 수행해보도록 하겠습니다.
3.5 *유사, 아핀, 투영 변환
유클리드 변환 외에도 3D 공간에서 여러 가지 변형이 있습니다. 유클리드 변환은 벡터의 길이와 각도를 유지합니다. 이는 모양을 변경하지 않고 강체를 그대로 움직이거나 회전시키는 것과 같습니다. 다른 종류의 변환은 모양을 바꾸며 모두 비슷한 매트릭스 표현을 가지고 있습니다.
1. Similarity transform (유사 변환)
유사 변환은 Euclidean 변환보다 하나 더 많은 자유도를 더 가집니다. 객체의 크기가 일정하게 조정될 수 있으며 매트릭스 표현은 다음과 같습니다.
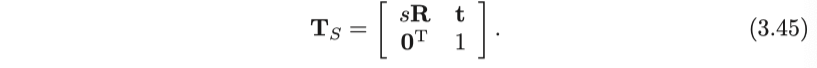
회전 부분은 벡터가 회전된 후 $x,\ y,\ z$ 의 좌표를 균등하게 스케일 할 수 있다는 것을 의미하는 스케일링 팩터 $s$를가집니다. 스케일링으로 인해 유사 변환은 더 이상 본체의 체적이 유지되지 않게 합니다. 한 변의 길이가 1 인 정육면체를 길이가 10 인 변 (즉, 정육면체)으로 변환한다고 상상할 수 있습니다. 3차원 유사 변환 집합은 $\mathrm{Sim}(3)$으로 표시되는 유사 변환 그룹이라고도 합니다.
2. Affine transform (아핀 변환)
아핀 변환의 행렬 형태는 다음과 같습니다.

유클리드 변환과는 달리, 아핀 변환은 가역 행렬이 될 필요가 있으며 반드시 직교 행렬이 될 필요는 없습니다. 아핀 변환은 직교 투영이라고도 합니다. 아핀 변환 후 큐브는 더 이상 사각형이 아니지만 각 면은 여전히 평행 사변형입니다.
3. Projective transform (투영 변환)
투영 변환은 가장 일반적인 변환이며 행렬 형식은 다음과 같습니다.
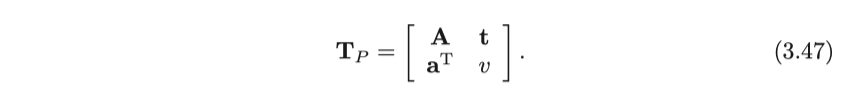
행렬의 왼쪽 위는 가역 행렬 A이고, 오른쪽 위는 변환 t이고, 왼쪽 아래는 스케일링 $\mathbf{a}^\mathrm{T}$이다. 우리가 동차 좌표를 사용하기 때문에, $v \neq 0$일 때, 전체 행렬을 $v$로 나눔으로써 오른쪽 하단 모서리가 1 인 행렬을 얻을 수 있고, 그렇지 않으면 우리는 오른쪽 하단 모서리가 0 인 행렬을 얻을 수 있습니다. 따라서 2D 투영 변환은 총 8 자유도를 가지며 3D는 총 15 자유도를 갖습니다. 투영 변환은 지금까지 말한 변형의 가장 일반적인 형태입니다. 실제 세계에서 카메라 사진으로의 변환은 투영 변환으로 볼 수 있습니다. 독자는 사진에서 정사각형 타일이 어떻게 생겼는지 상상할 수 있습니다. 이는 더 이상 정사각형이 아닙니다. 가까운 부분이 먼 부분보다 더 크기 때문에 평행 사변형이 아니라 불규칙한 사변형의 형태가 됩니다.
*역자 주: 이해를 돕기 위한 사진 (from Visual Navigation for Flying Robots Lecture)
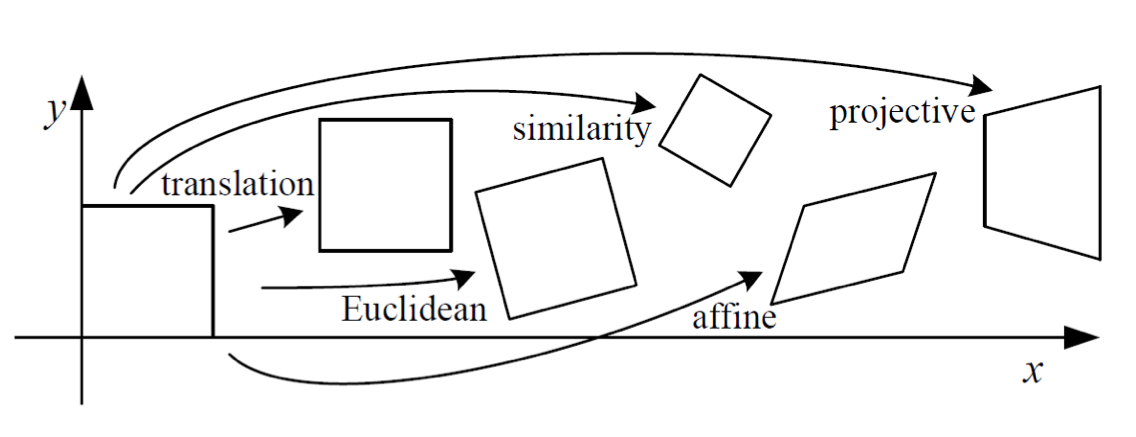
표 3-1에는 현재 다루는 여러 변환의 속성이 요약되어 있습니다. "Invariance"에는 위에서 아래로 포함 관계가 있습니다. 예를 들어, 볼륨을 유지하는 것 외에도 유클리드 변환은 parallelism, intersection 등의 속성을 갖습니다.

우리는 실제 세계로부터 카메라 사진으로의 변형이 원근법 변환이라는 것을 나중에 소개할 것입니다. 카메라의 초점 거리가 무한대이면 이 변환은 아핀 변환입니다. 그러나 카메라 모델에 대해 자세히 알아보기 전에 이러한 변환에 대한 대략적인 인상을 얻기 위해 몇 가지 실습을 해보겠습니다.
3.6 실습 : Eigen Geometry 모듈
3.6.1 Eigen geometry 모듈을 이용한 데모
자, 앞에서 언급 한 다양한 회전 표현식을 실제로 연습해 봅시다. Eigen에서 쿼터니언, 오일러 각 및 회전 행렬을 사용한 변환 방법을 소개할 것입니다. 또한 독자가 이러한 변형의 관계를 이해하는 데 도움이 되는 시각화 프로그램을 제시합니다.
slambook2/ch3/useGeometry/eigenGeometry.cpp
Eigen에서 표현의 다양한 형태는 아래에 요약되어 있습니다. 각 유형에는 single 및 double precision 데이터 유형이 모두 있으며 이전과 마찬가지로 컴파일러에서 자동으로 변환할 수 없습니다. 예를 들어 double precision을 사용하면 마지막 "d"를 "f"로 변경하여 single precision 데이터 구조를 얻을 수 있습니다.
- 회전 행렬 (3× 3) : Eigen :: Matrix3d.
- 회전 벡터 (3× 1) : Eigen :: AngleAxisd.
- 오일러 각 (3× 1) : Eigen :: Vector3d.
- 쿼터니언 (4 × 1) : Eigen :: Quaterniond.
- 유클리드 변환 행렬 (4 × 4) : Eigen :: Isometry3d.
- Affine 변환 (4 × 4) : Eigen :: Affine3d.
- 투영 변환 (4 × 4) : Eigen :: Projective3d.
이 프로그램은 "CMakeLists.txt"를 참조하여 컴파일할 수 있습니다. 이 프로그램에서 회전 행렬, 회전 벡터, 오일러 각, 그리고 쿼터니언을 어떻게 Eigen에서 사용하는지에 대해 실습합니다. 우리는 벡터 v를 회전시키기 위해 이러한 회전을 사용하고 결과가 같다는 것을 보입니다. 동시에 이러한 표현들이 프로그램에서 어떻게 변환되는지에 대해 실습합니다. Eigen의 지오메트리 모듈에 대해 더 자세히 알고 싶은 독자는 다음의 참고 문서를 참조할 수 있습니다 (eigen.tuxfamily.org/dox/group__TutorialGeometry.html)
프로그램 코드는 수학적 표현과의 미묘한 차이점을 가지고 있습니다. 예를 들어, C++에서 연산자 오버 로딩에 의해, 쿼터 니온 및 3차원 벡터를 직접 곱할 수 있지만 수학적으로 이 3차원 벡터는 우리가 마지막 섹션에서 이야기 한 것처럼 imaginary 쿼터니언으로 변환된 이후에 쿼터니온 곱셈이 계산에 사용됩니다. 동일한 형태가 변환 행렬에 3 차원 벡터에 곱한 값에 적용됩니다. 일반적으로 프로그램의 사용법은 수학 공식보다 유연하게 동작합니다.
3.6.2 좌표 변환 예제
좌표 변환을 보여주는 간단한 예를 들어 보겠습니다.
예제 1. 로봇 1 호와 로봇 2 호는 세계 좌표계 상에 위치해 있습니다. 우리는 세계 좌표계 $W$와 로봇 좌표계 $R_1 $, $R_2 $를 사용하고 있다고 가정합시다. 로봇 1호의 포즈는 $ \mathbf {q}_ 1 = [ 0.35, 0.2, 0.3, 0.1 ]^ \mathrm{T}, \mathbf{t}_ 1 = [ 0.3, 0.1, 0.1 ]^ \mathrm{T} $ 입니다. 로봇 2호의 포즈는 $ \mathbf{q}_2 = [ - 0.5, 0.4, - 0.1, 0.2 ]^ \mathrm{T}, \mathbf{t}_ 2 = [- 0.1, 0.5, 0.3 ]^ \mathrm{T} $ 입니다. $ \mathbf {q} $와 $ \mathbf{t} $는 세계 좌표계와 로봇 좌표계 사이의 변환 행렬 $ \mathbf{T}_{R_k, W}, k= 1, 2 $ 를 표현합니다. 로봇 1호가 자기 자신의 좌표계에서 한 점 $ \mathbf{p}_{R_1} = [ 0.5, 0, 0.2 ]^ \mathrm{T} $ 을 바라볼 때 이 점의 좌표를 이를 로봇 2호의 좌표계에 대해 계산하고자 한다고 해봅시다.
이것은 매우 간단하지만 대표적인 예입니다. 실제 시나리오에서는 동일한 로봇의 다른 부분이나 다른 로봇 사이에서 좌표를 변환해야 합니다. 아래에서는 이 계산을 보여주는 프로그램을 작성합니다.
slambook2/blob/master/ch3/examples/coordinateTransform.cpp
gaoxiang12/slambook2
edition 2 of the slambook. Contribute to gaoxiang12/slambook2 development by creating an account on GitHub.
github.com
프로그램의 답은 $ [- 0.0309731, 0.73499, 0.296108 ]^ \mathrm{T}$ 이며 계산 절차는 매우 간단합니다. 아래의 식을 계산하면 됩니다.
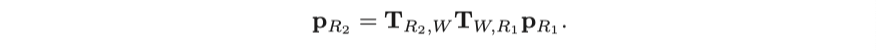
사용하기 전에 쿼터니언을 정규화해야 한다는 것을 기억하세요.
3.7 시각적 표현
3.7.1 궤적 그리기
회전 및 이동의 개념을 처음 사용하는 경우 양식이 조금 복잡해 보인다는 것을 알게 될 것입니다. 많은 표현 방법이 있으며 필요한 경우 기본적으로 선호하는 것으로 변환해야 합니다. 다행스럽게도 회전 및 변환 행렬의 값이 충분히 직관적이지 않을 수 있지만, 우리는 이를 3D 창에서 쉽게 그릴 수 있습니다.
이 섹션에서는 두 가지 시각적 예를 보여줍니다. 첫째, 우리는 어떤 방식 으로는 로봇의 궤적을 기록했으며 이제 우리는 그것을 그림에 그릴 것을 원합니다. 궤적 파일이 "trajectory.txt"라는 텍스트 파일에 저장되었고 각 라인은 다음의 포맷으로 저장된다고 가정해봅시다.

여기서 시간은 이 포즈의 기록 시간, t는 변환, q는 쿼터니언이며, 모두 세계 좌표계에서 로봇 좌표계에 기록됩니다. 아래에서 이 궤적을 파일에서 읽고 창에 표시합니다. 원칙적으로 "로봇 포즈"에 대해 이야기하면 $ \mathbf {T}_{WR} $ 또는 $ \mathbf {T}_{RW} $ 중 하나를 사용할 수 있습니다. 서로의 역이기 때문입니다. 그 중 하나를 아는 것은 다른 것을 쉽게 얻을 수 있음을 의미합니다. 로봇의 궤적을 저장하려면 $ \mathbf {T}_{WR} $ 또는 $ \mathbf {T}_{RW} $를 저장해도 큰 차이가 없습니다.
우리는 궤적을 점의 연속적인 집합으로 그려볼 것입니다. 엄밀히 말하면, 이것은 실제로 세계 좌표계에서 로봇의 원점의 좌표입니다. 로봇 좌표계의 원점 $ \mathbf {O}_{R}$을 고려하십시오. 즉, 이 시점에서 $ \mathbf{O}_{W}$는 세계 좌표계에서 원점의 좌표입니다.

이는 정확히 $ \mathbf {T}_{WR} $의 이동 변환 부분입니다. 따라서 우리는 $ \mathbf {T}_{WR} $ 수식으로부터 카메라가 공간상에서 어디에 있는지 정확히 알 수 있습니다. 따라서 대부분의 공개 데이터 세트에서 궤적 파일은 $ \mathbf {T}_{RW} $ 대신 $ \mathbf {T}_{WR} $을 저장합니다.
마지막으로 3D 그리기를 지원하는 라이브러리가 필요합니다. 유명한 MATLAB, Python Matplotlib, OpenGL 등과 같은 3D 그리기를 지원하는 많은 라이브러리들이 있습니다. Linux에서는 공통 라이브러리가 OpenGL 기반 Pangolin 라이브러리이며 OpenGL을 기반으로 일부 3D 그리기 작업을 제공합니다. 이 책의 두 번째 판에서는 Git의 서브 모듈 기능을 사용하여이 책이 의존하는 제3 자 라이브러리를 관리했습니다. 독자들은 필요한 라이브러리를 설치하기 위해 "3rdparty"폴더로 직접 이동할 수 있으며, Git는 사용 중인 버전과 일치하는 것을 보장합니다.
slambook2/blob/master/ch3/examples/plotTrajectory.cpp
gaoxiang12/slambook2
edition 2 of the slambook. Contribute to gaoxiang12/slambook2 development by creating an account on GitHub.
github.com
이 프로그램은 Pangolin에서 3D 포즈를 그리는 방법을 보여줍니다. 우리는 빨간색, 녹색 및 파란색으로 각 포즈의 세 축을 그립니다 (실제로 각 축의 세계 좌표를 계산 한 다음, 포즈를 검은색 선으로 연결합니다.) 결과는 그림 3-3에 나와 있습니다.

3.7.2 카메라 포즈 시각화
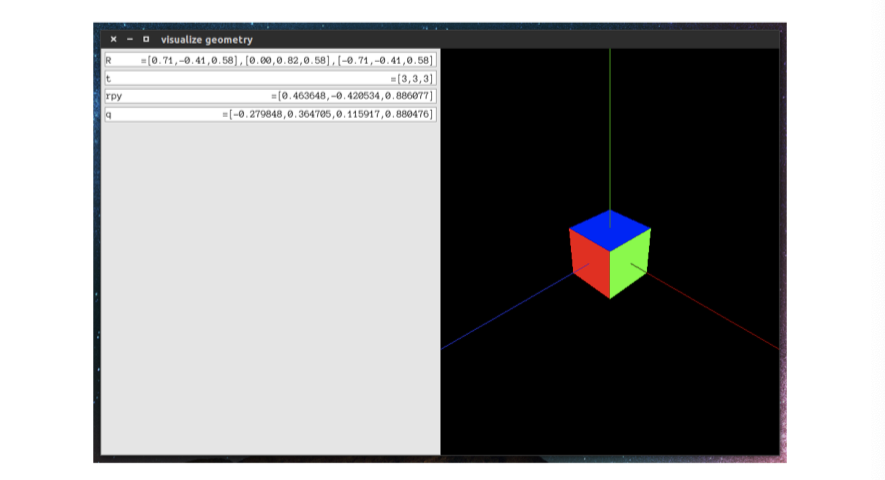
궤적을 표시하는 것 외에도 3D 창에 카메라의 포즈를 표시할 수도 있습니다. slambook2/ch3/visualizeGeometry에서는 카메라 포즈의 다양한 표현식을 시각화합니다 (그림 3-4 참조). 리더가 마우스를 사용하여 카메라를 움직이면 왼쪽의 상자가 회전 매트릭스, 번역, 오일러 각 및 카메라의 쿼터니언이 실시간으로 표시됩니다. 데이터가 어떻게 변경되는지 볼 수 있습니다. 우리의 경험에 따르면 쿼터니언이나 행렬에서 정확한 회전을 추론하기는 어렵습니다. 그러나 회전 행렬이나 변환 행렬은 직관적이지는 않지만 시각적으로 표시하는 것은 어렵지 않습니다. 이 프로그램은 Pangolin 라이브러리를 3D 디스플레이 라이브러리로 사용합니다. 프로그램을 컴파일하기 위해서는 "Readme.txt"를 참고하십시오.
연습문제
- 회전 행렬이 직교 행렬인지 확인하십시오.
- 로드리게스 수식의 유도 과정을 찾아서 이해하십시오.
- 쿼터니언이 3차원 점을 회전시킨 후에 결과가 3차원 공간 점에 해당하는 imaginary 쿼터니언임을 증명하십시오. (3.33 참고)
- 회전 행렬, 축 각도, 오일러 각 및 쿼터니온 간의 변환 관계를 요약하는 표를 그려보세요.
- Eigen 라이브러리에서 행렬이 있는 경우 왼쪽 위 구석의 3×3 블록의 값을 확인하고 $\mathbf{I}_{3 \times 3}$을 여기에 대입하고 싶습니다. 이를 달성하기 위한 C++ 프로그램을 구현하십시오.
- 일반 선형 방정식 Ax = b가 어떤 경우 유일한 해 x를 가집니까? 수치적으로 어떻게 이를 풀 수 있나요? Eigen 라이브러리를 활용하여 그것을 구현할 수 있습니까?
'입문 SLAM 14강 (번역)' 카테고리의 다른 글
| 입문 Visual SLAM 14강 : 5장. 카메라 및 이미지 (2) | 2021.04.19 |
|---|---|
| 입문 Visual SLAM 14강 : 4장. Lie군과 Lie 대수 (0) | 2021.03.25 |
| 입문 Visual SLAM 14강 : 참고문헌 (0) | 2021.02.17 |
| 입문 Visual SLAM 14강 : 2장. SLAM과의 첫만남 (0) | 2021.02.17 |
| 입문 Visual SLAM 14강 : 1장. 선행지식 (0) | 2021.02.17 |



